[latexpage]

By Ignacio Lopez-Gomez

Over the past few years, machine learning has become a fundamental component of some newly developed Earth system parameterizations. These parameterizations offer the potential to improve the representation of biological, chemical, and physical processes by learning better approximations derived from data. Parameters within data-driven representations are learned using some kind of algorithm, in a process referred to as model training or calibration. Gradient-based supervised learning is the dominant training method for such parameterizations, mainly due to the availability of efficient and easy-to-use open source implementations with extensive user bases (e.g., scikit-learn, TensorFlow, PyTorch). However, these learning algorithms impose strong constraints on the relation between the machine-learned parameterizations and the training data that are not always desirable in a climate modeling setting.

The most salient constraint of gradient-based supervised learning is the requirement that training data contain as targets differentiable functions of the parameterizations to be learned, which enables backpropagation of gradients of the mismatch between the targets and the model outputs. In the context of atmospheric dynamics, we only have access to indirect and noisy data about turbulent and cloud microphysical processes, so this requirement cannot be met. The same is true for other climate applications, where reliable measurements of what parameterizations should output are inaccessible.

Difficulties arising from the need to structure model training as a standard supervised learning problem compound as the parameterizations are integrated in a global Earth System Model. This results in situations where the learning goal needs to be adjusted to fit the training algorithm: many machine-learned parameterizations are trained to reduce errors in noisy short-time tendencies, even though the quantities of interest in climate modeling are long-term statistics. Reconciling the goals of climate modeling with gradient-based learning would require nothing short of subordinating the entire modeling effort to differentiability requirements. However, existing Earth System Models are not differentiable, both for physical reasons (e.g., at phase transitions) and numerical reasons (e.g., undesirable yet often unavoidable discontinuous numerical filters) (Shen et al, 2023). Even if they could be made differentiable, there remains vast climate-relevant information that cannot be structured in a supervised way, such as large-scale time-aggregated measurements of cloudiness. Leveraging all information at our disposal is crucial to constrain the uncertainty in climate projections.

To address these challenges and facilitate data-driven modeling in the climate setting, we propose two key modifications to the gradient-based supervised learning paradigm. First, we pose the machine learning task as an inverse problem. Second, we solve this inverse problem using a derivative-free approach.

In an inverse problem, we do not require the training data to contain the output of the parameterizations we seek to learn. Instead, we only assume that we can evaluate the mismatch between the available data and the forecast of a model that includes the parameterizations we are interested in. In this framework, the technical difficulties associated with training components of a large computational model shift to ensuring that the observed mismatch is informative about the processes that we want to parameterize; this problem can be addressed by combining domain knowledge with uncertainty quantification. In addition, the inverse problem setting has a Bayesian interpretation where observational and structural errors arise naturally, so it enables training models with noisy and multi-fidelity data.

Ensemble Kalman Processes

But what algorithms can be used to solve the inverse problems typical of climate modeling? We recently demonstrated the effectiveness of ensemble Kalman processes to tackle this task, training physics-based and neural network parameterizations within a state-of-the-art atmospheric turbulence and convection model (Lopez-Gomez et al, 2022).

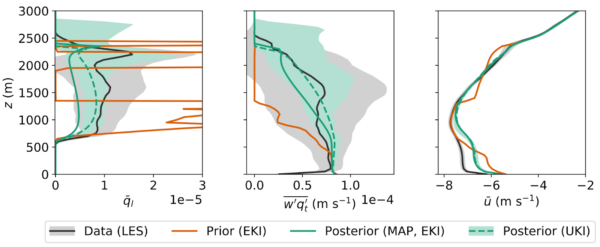
Ensemble Kalman processes are based on the ensemble Kalman filter, widely used as an effective method to sequentially correct forecasts made by weather models with the latest available data (Evensen et al, 1994). The robustness of the ensemble Kalman filter to noise in the data carries over to the climate modeling setting, where we can use ensemble Kalman processes to learn about parameterizations from noisy and chaotic trajectories of the climate system (Schneider et al, 2021; Huang et al, 2022). This enables us, for instance, to constrain turbulence and convection models from time-averaged statistics of cloud data. We showcase this example using two ensemble Kalman processes, ensemble Kalman inversion and unscented Kalman inversion, in Figure 1.

Uncertainty quantification enabled by ensembles

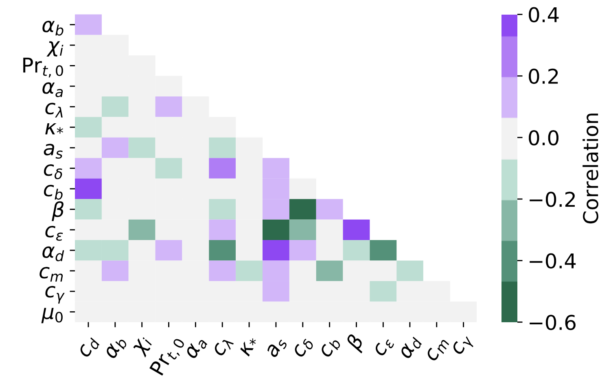
Ensemble Kalman processes not only allow learning best fitting point estimates of parameters within Earth system models. Through an appropriate choice of the ensemble Kalman algorithm, a Gaussian approximation to the posterior uncertainty is also returned by the learning process (Huang et al, 2022). This uncertainty estimate can be propagated to any output of the model, as demonstrated by the green shading in Figure 1. It also enables analyzing parameter correlations within the model (Figure 2), providing important insight that can be leveraged to further improve the model. For instance, Figure 2 reveals that the surface area fraction $a_s$ used in the calibrated model is highly correlated with other model parameters, suggesting that this parameter should be replaced by a function of the other parameters, which may be machine-learned.

For models where the parametric uncertainty is not expected to be Gaussian, more sophisticated sampling methods must be applied. Here, the parameter-output pairs generated by the ensemble Kalman process can be used as regression data for data-driven emulators like Gaussian processes, neural networks, or random feature models; these emulators can then be sampled to obtain the posterior uncertainty, as we discussed in this blog post.

An open source lightweight implementation in Julia

An important benefit of gradient-based solvers is the existence of efficient open source implementations. To begin leveling the playing field, we have recently released EnsembleKalmanProcesses.jl, a lightweight Julia implementation of the algorithms of the same name (Dunbar, Lopez-Gomez et al, 2022). Although the package is written in Julia, the non-intrusive nature of the algorithms enable the software to be used to learn parameters within models written in any language, including Fortran or Python. The only requirement is the ability to write the value of the parameters and the evaluated functions to a text file at each iteration of the learning process.

Parameterization learning as an inverse problem has already been applied successfully to models of atmospheric and oceanic turbulence and convection (Dunbar et al, 2021; Lopez-Gomez et al, 2022; Hillier, 2022), and atmospheric gravity waves (Mansfield & Sheshadri, 2022). At CliMA, current applications include learning about microphysical processes, constraining conceptual models of cloud regime transitions, and training stochastic parameterization. Stay tuned for more!